Двоичный поиск

Содержание

Введение
Описание алгоритма
Реализация двоичного поиска(рекурсия)
Реализация двоичного поиска(итерация)
Дополнительно. Получение всех вхождений
Оценка сложности алгоритма

Введение

В данной статье рассмотрим алгоритм двоичного поиска(бинарного поиска), реализуем его на языке программирования Go(Golang) и оценим сложность алгоритма используя O-большое.

Описание алгоритма

Основная идея двоичного поиска заключается в последовательном делении отсортированного массива на две части, для этого выбирается элемент в середине массива и сравнивается с искомым значением, если значения равны, то поиск завершается. Если же элементы не равны, то необходимо повторить деление одной из двух полученных частей. В случае, когда выбранный элемент меньше искомого, необходимо повторить деление для правой части, иначе деление повторяется для левой. Алгоритм повторяется до тех пор пока не будет найдено значение или не закончатся элементы для сравнения. Разберем описанное на конкретном примере:

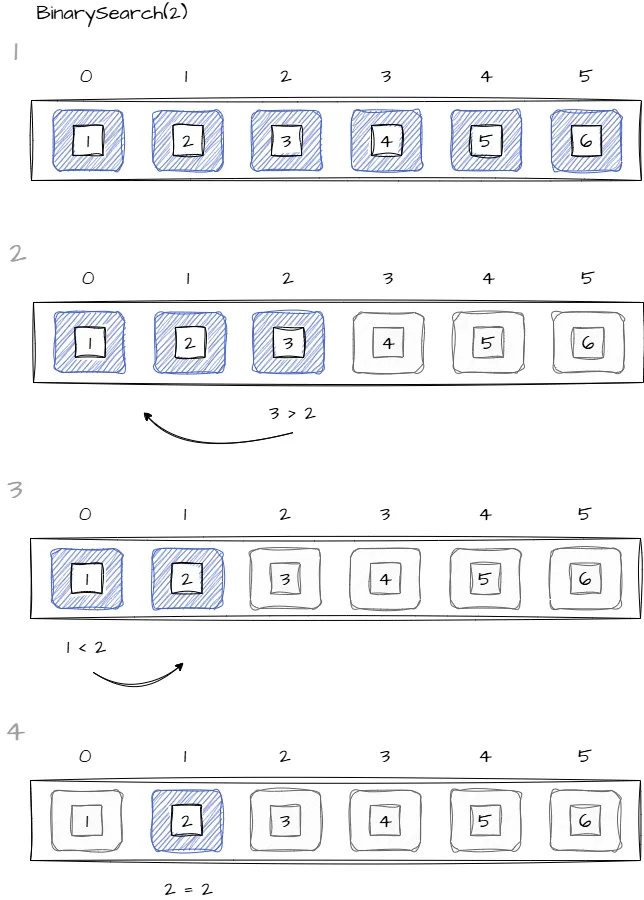
Изображение иллюстрирует алгоритм двоичного поиска

Реализация двоичного поиска(рекурсия)

Реализуем алгоритм рекурсивным методом, в данном варианте поиск происходит за счет передачи полученной после деления части массива в качестве аргумента той же самой функции. Рекурсивные вызовы происходят пока элемент не будет найден или не закончаться элементы для сравнения.

123456789101112131415161718192021222324252627

// Реализация бинарного поиска, рекурсивный вариант.
// array - отсортированный массив
// value - значение для поиска в массиве array
func BinarySearch(array []int, value int) int {
  end := len(array) - 1
  if end >= 0 {
    // Вычисление середины массива
    index := end / 2
    // Если значения равны, значит удалось найти элемент
    if array[index] == value {
      return index
      // Если выбранный элемент больше, то переходим в левую часть
    } else if array[index] > value {
      if result := BinarySearch(array[:index], value); result >= 0 {
        return result
      }
      // Если выбранный элемент меньше, то переходим в правую часть
    } else if array[index] < value {
      begin := index + 1
      if result := BinarySearch(array[begin:end+1], value); result >= 0 {
        return begin + result
      }
    }
  }
  // Если значение не найдено в массиве
  return -1
}

Реализация двоичного поиска(итерация)

Любой рекурсивный алгоритм может быть представлен в итеративном стиле, то есть, с использованием циклов, давайте рассмотрим следующий вариант с использованием цикла.

12345678910111213141516171819202122232425

// Реализация бинарного поиска, итеративный вариант.
// array - отсортированный массив
// value - значение для поиска в массиве array
func BinarySearch(array []int, value int) int {
  index := 0
  begin := 0
  end := len(array) - 1

  for begin <= end {
    // Вычисление середины массива
    index = (begin + end) / 2
    // Если значения равны, значит удалось найти элемент
    if array[index] == value {
      return index
      // Если выбранный элемент больше, то переходим в левую часть
    } else if array[index] > value {
      end = index - 1
      // Если выбранный элемент меньше, то переходим в правую часть
    } else if array[index] < value {
      begin = index + 1
    }
  }
  // Если значение не найдено в массиве
  return -1
}

Чаще всего реализация через итеративный подход является предпочтительнее, так как, требует меньше ресурсов и работает быстрее.

Дополнительно. Получение всех вхождений

Предыдущие варианты возвращали ответ при первом совпадении, но часто требуется найти все вхождения значения в массив. Перепишем код таким образом, чтобы результатом был массив с индексами всех вхождений указанного значения.

1234567891011121314151617181920212223242526272829303132333435363738394041

// Реализация бинарного поиска, поиск всех вхождений.
// array - отсортированный массив
// value - значение для поиска в массиве array
func BinarySearch(array []int, value int) []int {
  index := 0
  begin := 0
  end := len(array) - 1

  result := []int{}
  for begin <= end {
    // Вычисление середины массива
    index = (begin + end) / 2
    // Если значения равны, значит удалось найти элемент
    if array[index] == value {
      result = append(result, index)

      // Двигаемся влево до тех пор пока значения совпадают и есть элементы
      leftIndex := index - 1
      for leftIndex >= begin && array[leftIndex] == value {
        result = append(result, leftIndex)
        leftIndex--
      }

      // Двигаемся вправо до тех пор пока значения совпадают и есть элементы
      rightIndex := index + 1
      for rightIndex <= end && array[rightIndex] == value {
        result = append(result, rightIndex)
        rightIndex++
      }
      break
      // Если выбранный элемент больше, то переходим в левую часть
    } else if array[index] > value {
      end = index - 1
      // Если выбранный элемент меньше, то переходим в правую часть
    } else if array[index] < value {
      begin = index + 1
    }
  }
  // Если значение не найдено в массиве
  return result
}

Код выше работает в основном по тому же принципу, что и итеративный вариант реализации, единственное отличие в том, что после нахождения совпадения, необходимо проверить рядом стоящие элементы, и если они тоже совпадают добавить их индекс к результату.

Оценка сложности алгоритма

Количество элементов для сравнения на каждом шаге алгоритма уменьшается ровно в два раза, что соответствует формуле двоичного логарифма, и описывается как O(log n). Ниже приведена таблица для всех описанных вариантов.

Реализация	Сложность в O-нотации
Рекурсивный алгоритм	O(log n)
Итеративный алгоритм	O(log n)
Получение всех вхождений	O(log n + l + r)

Обратите внимание на то, что получение всех вхождений имеет отличную от других вариантов сложность, это связано с тем, что после нахождения первого вхождения необходимо последовательно найти все оставшиеся элементы, l - количество совпавших элементов слева, r - количество совпавших элементов справа.

Весь исходный код примеров к данной статье вы можете найти на GitHub.