Хеш-таблица
Содержание
Введение
В данной статье рассмотрим структуру данных хеш-таблица и реализуем ее на языке Go(Golang).
Описание структуры данных
Хеш-таблица, это структура данных, которая хранит элементы в паре ключ:значение, где ключ используется для доступа к ассоциируемым с ним значением. Для хранения данных используется массив, чтобы получить доступ к значению ячейки массива необходимо вычислить ее индекс на основе значения хеш-функции ключа. Данная структура данных реализует следующие основные операции: добавление, удаление и поиск по ключу. Ниже приведен пример упрощенной структуры хеш-таблицы:
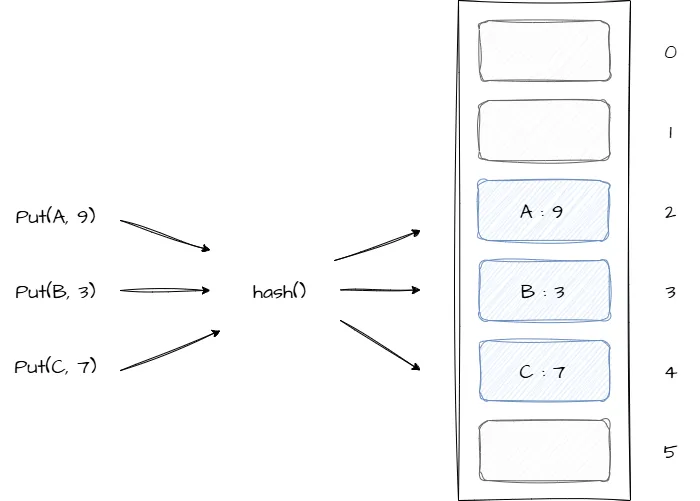
Так как в основе хеш-таблицы лежит массив, то все основные операции с этой структурой данных выполняются за O(1) при использовании достаточно быстрой хеш-функции. В данной статье в качестве хеш-функции используется реализация на основе djb2, ниже приведен ее код:
// Константы для алгоритма хеширования djb2.
const DJB2_SHIFT = 5
const DJB2_INIT_HASH = 5381
// Простая реализация хеш-функции на базе алгоритма djb2.
func hash(value any) uint64 {
text := fmt.Sprint(value)
hash := uint64(DJB2_INIT_HASH)
for _, symbol := range text {
hash = ((hash << DJB2_SHIFT) + hash) + uint64(symbol)
}
return hash
}
Вне зависимости от того насколько хорошо реализована хеш-функция, получаемый в итоге индекс ячейки для разных ключей может совпадать, как часто это будет происходить зависит от самой хеш-функции и количества элементов в массиве. Подобные совпадения индексов называют коллизиями, есть различные способы их устранения, в последующих главах рассмотрим наиболее часто используемые.
Закрытая адресация
Основная идея закрытой адресации заключается в том, что ячейка массива содержит не добавленные данные, а другую структуру данных, которая хранит все элементы с дублирующимся значением хеш-функции ключа. На практике в качестве таких структур данные чаще всего выступает связный список или обычный массив. В данном разделе рассмотрим реализацию на основе связного списка, которую еще называют методом цепочек. Ниже представлена диаграмма описывающая общую структуру хеш-таблицы реализованной с использованием метода цепочек:
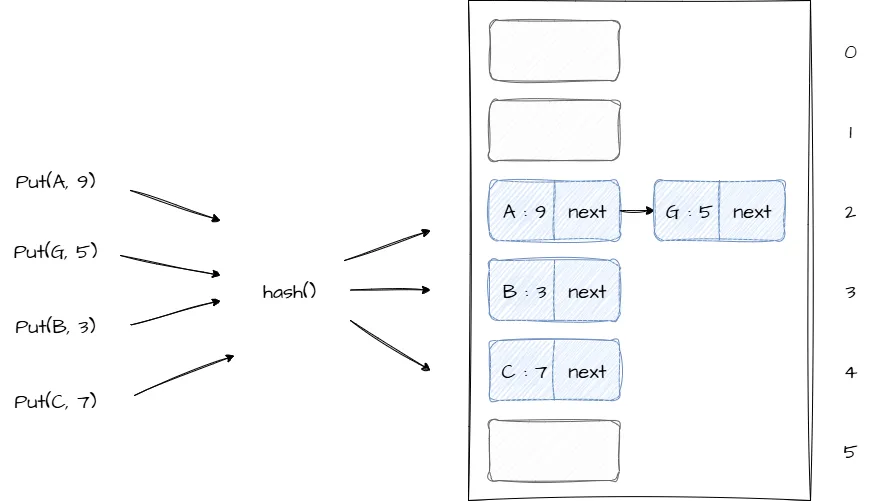
Объявление хеш-таблицы реализованной методом цепочек в коде выглядит следующим образом:
// Упрощенная реализация связного списка для хеш-таблицы.
type HashTableNode[K comparable, V any] struct {
key K
value V
next *HashTableNode[K, V]
}
// Реализация хеш-таблицы закрытой адресации методом цепочек.
type HashTable[K comparable, V any] struct {
size uint64
values []*HashTableNode[K, V]
}
Как показано на изображении выше в случае коллизии элемент добавляется следующим узлом в связный список. Со временем в хеш-таблице станет больше элементов, а значит и больше коллизий из-за чего количество узлов связного списка будет расти. Длина связного списка в значительной степени влияет на скорость операций хеш-таблицы, так как, для выполнения основных операций требуется перебрать узлы списка, время выполнения операций будет деградировать до времени выполнения операций связного списка, то есть до O(n). Для решения данной проблемы необходимо отслеживать уровень заполнения хеш-таблицы и в случае достижения определенного уровня копировать массив хеш-таблицы в новый, но уже большего размера. В реализации к данной статье копирование происходит при достижении уровня заполнения 0.75, где 1.0 хеш-таблица заполнена полностью, текущий уровнь заполнения расчитывается по формуле кол-во элементов / кол-во ячеек массива. Ниже приведена реализация добавления элемента:
// Начальный размер хеш-таблицы
const INIT_SIZE = 100
// Уровень заполнености при котором произойдет выделение нового места
const LOAD_FACTOR = 0.75
// Значение на которое будет увеличен размер таблицы
const INCREASE_FACTOR = 2
// Добавление элемента в хеш-таблицу.
// key - ключ
// value - значение
func (htable *HashTable[K, V]) Put(key K, value V) {
// Инициализация при первом обращении
if htable.values == nil {
htable.values = make([]*HashTableNode[K, V], INIT_SIZE)
} else {
// Если таблица заполнена больше, чем на LOAD_FACTOR,
// необходимо перенести данные в таблицу большего размера
loaded := float64(htable.size) / float64(len(htable.values))
if loaded >= LOAD_FACTOR {
values := htable.values
htable.values = make([]*HashTableNode[K, V], htable.size*INCREASE_FACTOR)
htable.size = 0
// Перехеширование всех элементов таблицы
for _, node := range values {
for node != nil {
htable.Put(node.key, node.value)
node = node.next
}
}
}
}
// Вычисление индекса на основе хеш-функции
index := hash(key) % uint64(len(htable.values))
if htable.values[index] == nil {
htable.values[index] = &HashTableNode[K, V]{key: key, value: value}
// Если ячейка уже содержит элемент, то необходимо найти последний узел списка
// и добавить новый элемент
} else {
node := htable.values[index]
for node.next != nil && node.key != key {
node = node.next
}
if node.key != key {
node.next = &HashTableNode[K, V]{key: key, value: value}
}
}
htable.size++
}
В строках 8-19 происходит проверка уровня заполнения, если он достиг значения константы LOAD_FACTOR, то происходит копирование всех элементов с перехешированием каждого из них. Код в строках 27-36 выполняется в случае возникновения коллизии, узлы списка перебираются до тех пор пока не будет достигнут конец списка, обратите внимание на условие node.key != key, оно позволяет избежать дублей в хеш-таблице.
Прежде чем удалить элемент потребуется сперва найти ячейку массива и узел списка в котором хранится удаляемый элемент, для удаления необходимо, чтобы предыдущий узел начал ссылаться на следующий за удаляемым, код удаления элемента из хеш-таблицы показан ниже:
// Удаление значения по указанному ключу.
// key - ключ для поиска значения в хеш-таблице
func (htable *HashTable[K, V]) Delete(key K) {
if htable.values != nil {
index := hash(key) % uint64(len(htable.values))
var prev *HashTableNode[K, V]
node := htable.values[index]
for node != nil {
// Если найден удаляемый элемент
if node.key == key {
if prev != nil {
prev.next = node.next
// Если удаляемый элемент единственный узел в списке
} else {
htable.values[index] = node.next
}
break
}
prev = node
node = node.next
}
htable.size--
}
}
В строках 7-20 происходит поиск удаляемого элемента, если элемент найден, то он удаляется, в противном случае поиск завершается достигнув конца связного списка.
Поиск элемента реализуется схожим образом, требуется найти ячейку массива и узел в котором хранится элемент, код ниже реализует поиск элемента по ключу:
// Получение значения по ключу.
// key - ключ для поиска значения в хеш-таблице
func (htable *HashTable[K, V]) Get(key K) V {
var result V
if htable.values != nil {
index := hash(key) % uint64(len(htable.values))
node := htable.values[index]
for node != nil {
if node.key == key {
result = node.value
break
}
node = node.next
}
}
return result
}
Открытая адресация
Открытая адресация хранит данные в ячейках массива без использования вспомогательных структур данных, а при возникновении коллизий переносит добавляемый элемент в свободную ячейку массива. Для определения свободной ячейки используется один из следующих алгоритмов:
Линейное пробирование
Алгоритм заключается в последовательном смещении на одну ячейку до тех пор пока не будет найдена свободная, ниже представлен поиск свободной ячейки с использованием линейного пробирования:
index := hash(key) % uint64(len(htable.values))
for htable.values[index] != nil && htable.values[index].key != key {
index++
index %= uint64(len(htable.values))
}
Со временем скорость операций с использованием линейного пробирования значитаельно ухудшается, связанно это с тем, что все добавляемые элементы следуют друг за другом в массиве и требуется все больше итерация для поиска ячейки, подобное поведение называют группировкой.
Квадратичное пробирование
При проверке ячеек массива квадратичное пробирование выбирает следующую ячейку на основании квадрата номера шага проверки, последовательность при проверке начиная с первой ячейки массива будет следующей: 1, 4, 9, 16 и т.д.. Реализация квадратичного пробирования представлена далее:
index := hash(key) % uint64(len(htable.values))
for htable.values[index] != nil && htable.values[index].key != key {
index = (index * index)
index %= uint64(len(htable.values))
}
В меньшей степени, но квадратичное пробирование подверженно группировкам как и линейное, так как для одного и того же индекса алгоритм генерирует одинаковую последовательность. Для элементов с совпадающем хеш-значением требуется больше итераций для поиска свободной ячейки.
Двойное хеширование
Основная проблема линейного и квадратичного пробирования заключается в образовании групп, алгоритм двойного хеширования позволяет этого избежать благодаря генерации разной последовательности смещений для совпадающих хеш-значений. Достигается это путем повторного хеширования полученного индекса, как пример следующим образом: смещение = константа - индекс % константа, данный подход будет использован для реализации хеш-таблицы в данной главе.
На иллюстрации ниже приведен пример упрощенной структуры хеш-таблицы с открытой адресацией:
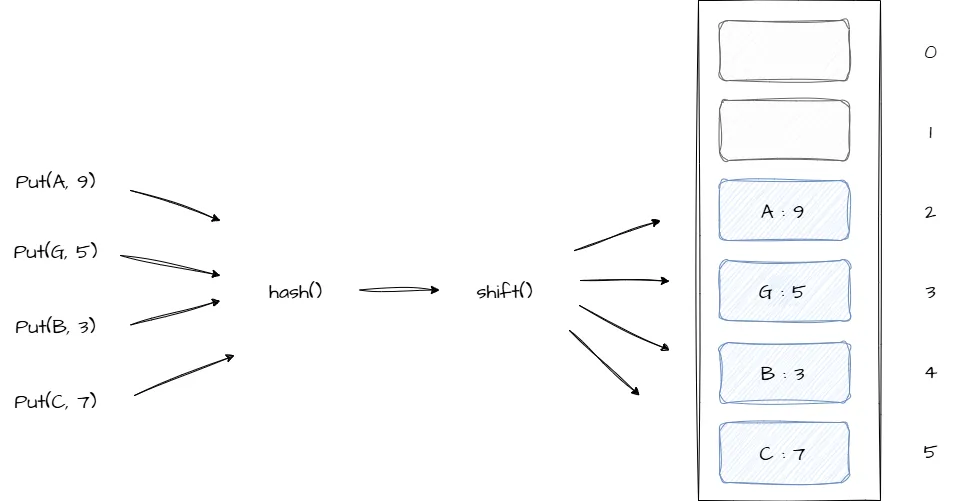
Хеш-таблица с открытой адресацией может быть объявлена следующим образом:
// Узел для хранения данных хеш-таблицы.
type HashTableNode[K comparable, V any] struct {
key K
value V
}
// Реализация хеш-таблицы открытой адресации с использованием двойного хеширования.
type HashTable[K comparable, V any] struct {
size uint64
values []*HashTableNode[K, V]
}
При добавлении элемента в хеш-таблицу с использованием двойного хеширования вычисляется индекс и сдвиг shift на основании индекса, который будет использоваться для поиска свободной ячейки в случае коллизии, операция добавления элемента показана ниже:
// Начальный размер хеш-таблицы
const INIT_SIZE = 100
// Уровень заполнености при котором произойдет выделение нового места
const LOAD_FACTOR = 0.5
// Значение на которое будет увеличен размер таблицы
const INCREASE_FACTOR = 2
// Добвление элемента в хеш-таблицу.
// key - ключ
// value - значение
func (htable *HashTable[K, V]) Put(key K, value V) {
// Инициализация при первом обращении
if htable.values == nil {
htable.values = make([]*HashTableNode[K, V], INIT_SIZE)
} else {
// Если таблица заполнена больше, чем на LOAD_FACTOR,
// необходимо перенести данные в таблицу большего размера
loaded := float64(htable.size) / float64(len(htable.values))
if loaded >= LOAD_FACTOR {
values := htable.values
htable.values = make([]*HashTableNode[K, V], htable.size*INCREASE_FACTOR)
htable.size = 0
// Перехеширование всех элементов таблицы
for _, node := range values {
if node != nil {
htable.Put(node.key, node.value)
}
}
}
}
index := hash(key) % uint64(len(htable.values))
// Вычисление сдвига относительно текущего индекса
shift := DJB2_SHIFT - index%DJB2_SHIFT
for htable.values[index] != nil && htable.values[index].key != key {
index += shift
index %= uint64(len(htable.values))
}
htable.values[index] = &HashTableNode[K, V]{key: key, value: value}
htable.size++
}
В строках 8-19 происходит проверка уровня заполнения, аналогичная приведенной в предыдущей главе. Поиск ячейки для вставки происходит в строках 24-27 и выполняется до тех пор пока не будет найдена пустая ячейка или совпадающее значение ключа, которое будет заменено на новое значение в строке 28.
Для удаления элемента необходимо двигаться по массиву использую полученный сдвиг до тех пор пока не будет найден удаляемый элемент или пока не будет достигнута свободная ячейка, как показано ниже:
// Удаление значения по указанному ключу.
// key - ключ для поиска значения в хеш-таблице
func (htable *HashTable[K, V]) Delete(key K) {
if htable.values != nil {
index := hash(key) % uint64(len(htable.values))
// Вычисление сдвига относительно текущего индекса
shift := DJB2_SHIFT - index%DJB2_SHIFT
for htable.values[index] != nil {
if htable.values[index].key == key {
htable.values[index] = nil
break
}
index += shift
index %= uint64(len(htable.values))
}
htable.size--
}
}
Получение элемента по ключу реализуется аналогичным образом, код приведен далее:
// Получение значения по ключу.
// key - ключ для поиска значения в хеш-таблице
func (htable *HashTable[K, V]) Get(key K) V {
var result V
if htable.values != nil {
index := hash(key) % uint64(len(htable.values))
// Вычисление сдвига относительно текущего индекса
shift := DJB2_SHIFT - index%DJB2_SHIFT
for htable.values[index] != nil {
if htable.values[index].key == key {
result = htable.values[index].value
break
}
index += shift
index %= uint64(len(htable.values))
}
}
return result
}
Сравнение реализаций
Все операции хеш-таблицы выполняются за O(1) вне зависимости от того используется открытая или закрытая адресация, тем не менее необходимо учитывать, что реализации на основе закрытой адресации требуют больше памяти для своей работы, так как используют вспомогательную структуру данных. Использование вспомогательной структуры данных может существенно упростить реализацию хеш-таблицы в случае, когда есть готовая реализация на которую возможно переложить часть логики.
Весь исходный код примеров к данной статье вы можете найти на GitHub.
