Алгоритм Кнута-Морриса-Пратта
Содержание
- Введение
- Общие сведения
- Этап 1. Префикс функция
- Этап 2. Реализация поиска
- Дополнительно. Поиск всех вхождений
Введение
В данной статье рассмотрим алгоритм Кнута-Морриса-Пратта, реализуем его на языке Go(Golang) и оценим сложность алгоритма используя O-большое.
Общие сведения
Алгоритм Кнута-Морриса-Пратта используется для поиска подстроки в тексте, и является более эффективным в сравнении с наивным поиском который сравнивает каждый символ подстроки и текста. Вместо этого данный алгоритм предлагает вычислить значение префикс функции, чтобы в случае несовпадения символов использовать полученное значение для определения ближайшего символа с которым может быть продолжено сравнение, для наивного алгоритма это всегда первый символ подстроки, что оказывает значительное влияние на время работы поиска. В общем виде алгоритм Кнута-Морриса-Пратта состоит из двух этапов: вычисление значения префикс функции и поиск по тексту с использование полученного значения на первом этапе.
Этап 1. Префикс функция
Префикс функцией строки str является массив целых чисел pfx, где элемент массива pfx[i] это максимальная длина собственного префикса подстроки str[0…i], который также является суффиксом подстроки str[0…i]. Рассмотрим пример вычисления префикс функции.
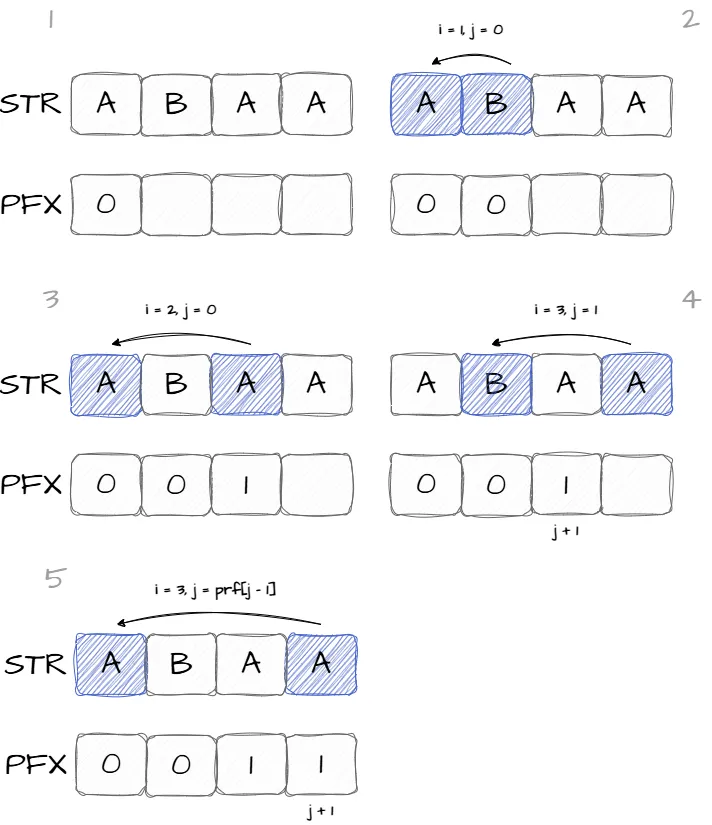
На изображении выше сравниваются символы строки str[i] и str[j], если символы равны, то в ячейку массива pfx[i] будет записано значение j + 1. В случае когда символы не равны и j равно 0 в ячейку массива pfx[i] записывается значение 0. Однако, если значение j больше 0, тогда потребуется изменить значение j на значение ячейки pfx[j-1] и продолжить сравнение символов. Описанный алгоритм префикс функции указанной строки может быть реализован следующим образом:
// Вычисление префикс функции.
// str - список символов для вычисления префикс функции
func Prefix(str []rune) []int {
prf := make([]int, len(str))
j := 0
i := 1
for i < len(str) {
// Если символы равны, то переходим к следующим
// символам для сравнения
if str[i] == str[j] {
prf[i] = j + 1
i++
j++
} else {
// Если символы не равны и j равен 0, то переходим
// к следующему символу для сравнения
if j == 0 {
i++
// Если символы не равны и j больше 0, то переходим
// используем полученное значение префикс функции для
// определения j
} else {
j = prf[j-1]
}
}
}
return prf
}
Данная реализация работает за O(n), где n - длина указанной строки.
Этап 2. Реализация поиска
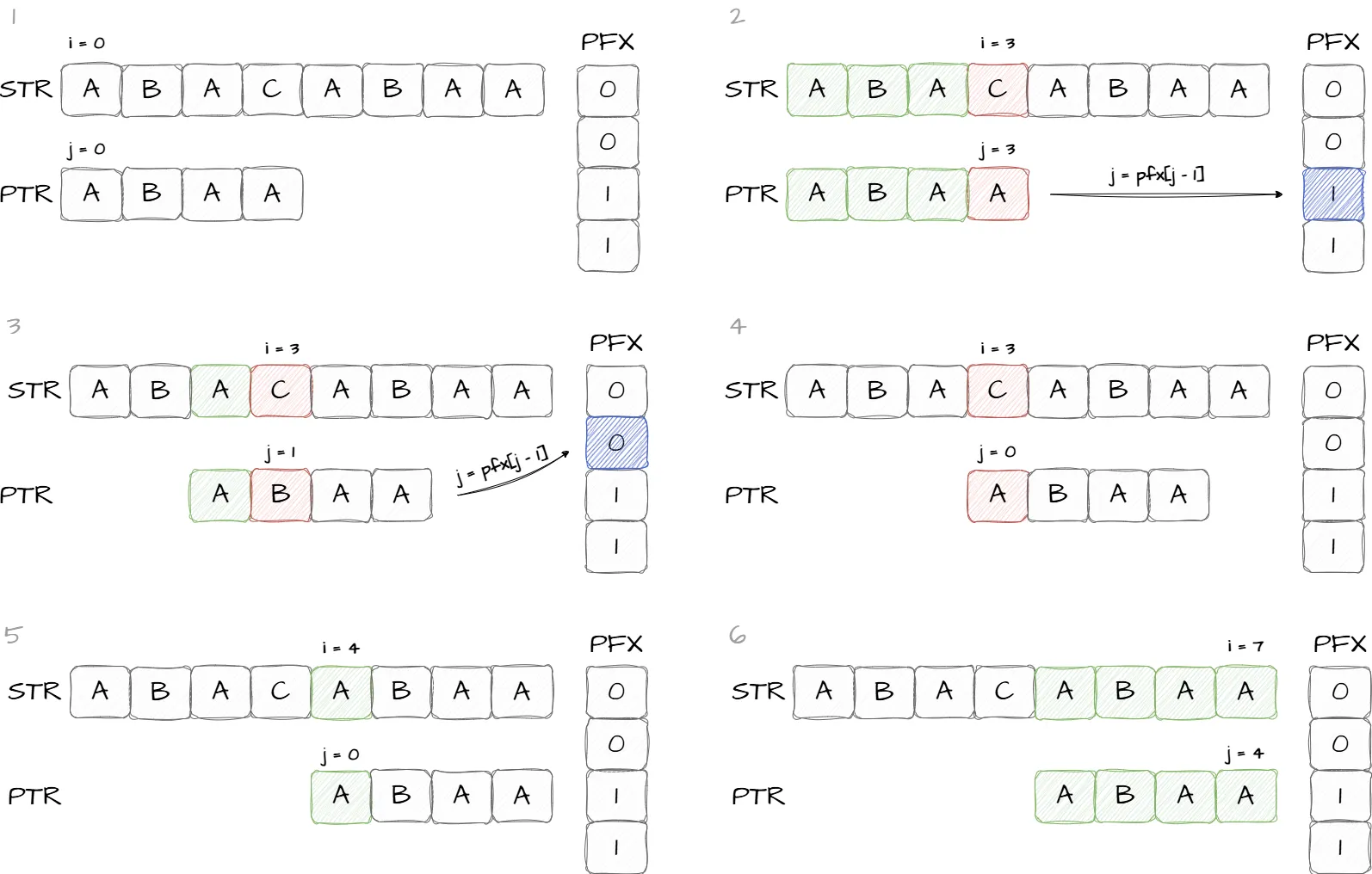
Получив значение префикс функции подстроки алгоритм поиска сводится к следующим шагам:
Символ подстроки ptr[j] сравнивается с символом текста str[i], если символы равны, то необходимо перейти к сравнению следующих символов, как только значение j достигает длины подстроки поиск считается успешным и его можно завершить. В случае когда символ ptr[j] не равен str[i] происходит переход к шагу 2.
Если символы ptr[j], str[i] не равны и значение j равно 0, тогда значение i сдвигается на единицу и алгоритм возвращается к шагу 1, в ином случае алгоритм переходит к шагу 3.
Если символы ptr[j], str[i] не равны и значение j больше 0, необходимо использовать значение префикс функции, чтобы найти следующий символ для сравнения присвоив значение pfx[j-1] индексу j, и далее продолжить поиск перейдя к шагу 1.
Изображение ниже иллюстрирует описанные шаги на примере:
Поиск может быть реализован следующим образом:
// Поиск первого вхождения подстроки с использованием
// алгоритма Кнута-Морриса-Пратта.
// str - строка в которой будет происходить поиск
// ptr - искомая подстрока
func Search(str []rune, ptr []rune) int {
prf := Prefix(ptr)
size := len(ptr)
i := 0
j := 0
for i < len(str) {
// Если символы равны, то переходим к сравнению
// следующих символов
if str[i] == ptr[j] {
i++
j++
// Если j достиг длины ptr, то подстрока
// найдена и поиск завершается
if j == size {
return i - size
}
} else {
// Если символы не равны и j = 0, переходим к
// следующему символу текста
if j == 0 {
i++
// Если символы не равны и j > 0, находим новое
// значение для j используя значение префикс функции
} else {
j = prf[j-1]
}
}
}
return -1
}
В строках 14-23 сравниваются символы искомой подстроки и текста, если индекс j достиг длины подстроки, то поиск завершается, что соответствуют шагу 1 из описания выше. В строках 26-30 происходит инкремент индекса i в том случае, если индекс j равен 0, данное условие аналогично шагу 2. Строки 30-32 соответствуют шагу 3, который использует значение префикс функции для поиска следующего значения индекса j.
Поиск подстроки в данной реализации выполняется за O(m + n), где O(n) это вычисление префикс функции, а O(m) поиск подстроки в тексте.
Дополнительно. Поиск всех вхождений
Чтобы найти все вхождения подстроки в текст используя алгоритм Кнута-Морриса-Пратта потребуются незначительные изменения кода приведенного выше. Когда индекс j достигает значения равного длине подстроки необходимо добавить значение в массив и продолжить сравнение с первого символа подстроки. Поиск всех вхождений может быть реализован следующим образом:
// Поиск всех вхождений подстроки с использованием
// алгоритма Кнута-Морриса-Пратта.
// str - строка в которой будет происходить поиск
// ptr - искомая подстрока
func SearchAll(str []rune, ptr []rune) []int {
prf := Prefix(ptr)
size := len(ptr)
res := []int{}
i := 0
j := 0
for i < len(str) {
// Если символы равны, то переходим к сравнению
// следующих символов
if str[i] == ptr[j] {
i++
j++
// Если j достиг длины ptr, то необходимо добавить значение в res
if j == size {
res = append(res, i-size)
j = 0
i++
}
} else {
// Если символы не равны и j = 0, переходим к
// следующему символу текста
if j == 0 {
i++
// Если символы не равны и j > 0, находим новое
// значение для j используя значение префикс функции
} else {
j = prf[j-1]
}
}
}
return res
}
В строках 20-24 заключается главное отличие от реализации представленной в предыдущем разделе, поиск не завершается с нахождением единственного соответствия, а продолжается до конца текста. Данная реализация выполняется за O(m + n), как и поиск первого вхождения приведенный ранее, но требует дополнительной памяти для хранения найденных индексов.
Весь исходный код примеров к данной статье вы можете найти на GitHub.
