Очередь

Содержание

1. Введение
2. Описание структуры данных
3. Реализация очереди(связный список)
4. Реализация очереди(массив)
5. Сравнение реализаций

Введение

В данной статье рассмотрим структуру данных очередь(Queue), реализуем ее на языке Go(Golang) и оценим сложность операций используя O-большое.

Описание структуры данных

Очередь в информатике работает по принципу FIFO(First-In-First-Out), то есть, элемент добавленный первым и покинет очередь первым, за ним второй и так далее до самого конца очереди. Для работы с очередью используются две основные операции добавление и удаление. В данной статье мы рассмотрим базовый вариант очереди, который может быть реализован на основе массива или связного списка.

Реализация очереди(связный список)

В реализации очереди на основе связного списка элементы хранятся в узлах списка, узлы следуют в порядке добавления новых элементов в очередь, ниже иллюстрируется структура очереди:

Изображение иллюстрирует структуру очереди на основе связного списка

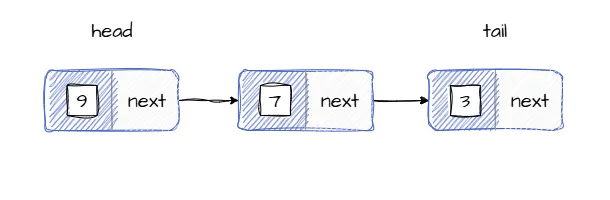
Код далее демонстрирует объявление очереди и упрощенную реализацию связного списка:

// Узел списка для хранения значения и указателя на следующий узел.
// value - значение в узле
// next  - указатель на следующий узел
type QueueNode[T any] struct {
  value T
  next  *QueueNode[T]
}

// Очередь на основе связного списка.
// head - указатель на первый узел списка
// tail - указатель на последний узел списка
type Queue[T any] struct {
  head *QueueNode[T]
  tail *QueueNode[T]
}

QueueNode - узел связного списка, хранит данные в поле value и указатель на следующий узел next.

Queue - очередь на основе связного списка, содержит указатели на первый и последний узлы очереди.

Для того, чтобы добавить новый элемент в очередь необходимо присвоить новый узел указателю tail:

1. Создать новый экземпляр QueueNode.

2. Указатель next последнего узла должен ссылаться на новый узел.

3. Указатель tail должен ссылаться на новый узел.


Изображение иллюстрирует добавление элемента в очередь

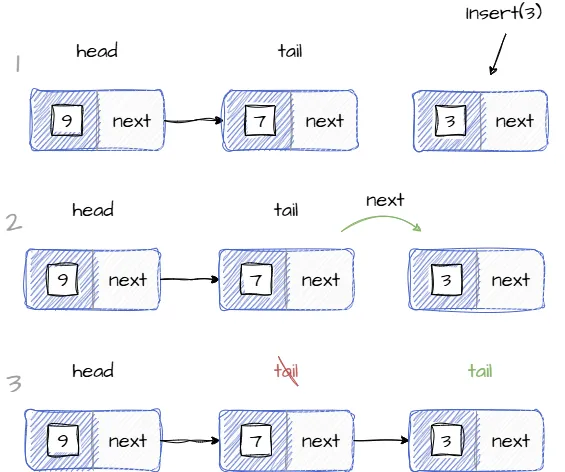
Код ниже реализует операцию добавления нового элемента в конец очереди:

1234567891011

// Добавление нового элемента в конец очереди.
// element - добавляемый элемент
func (queue *Queue[T]) Insert(element T) {
  node := &QueueNode[T]{value: element}
  if queue.tail != nil {
    queue.tail.next = node
  } else {
    queue.head = node
  }
  queue.tail = node
}

В строках 7-9 указатель head начинает ссылаться на новый узел в том случае, если очередь была пуста.

Удаление элемента из очереди производится заменой значения указателя head на значение его next.


Изображение иллюстрирует удаление элемента из очереди

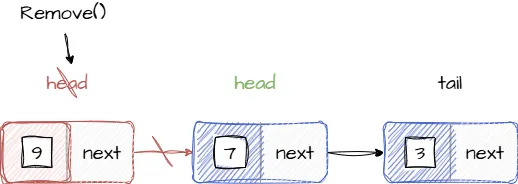
Код далее реализует удаление первого элемента из очереди:

1234567891011121314

// Удаление элемента из очереди, возвращает значение первого элемента или
// выбрасывает ошибку, если очередь пуста.
func (queue *Queue[T]) Remove() T {
  if queue.head != nil {
    value := queue.head.value
    queue.head = queue.head.next

    if queue.head == nil {
      queue.tail = nil
    }
    return value
  }
  panic("queue is empty")
}

В строках 8-10 указателю tail присваивается значение NULL если после удаления узла список оказывается пуст.

Реализация очереди(массив)

В данной реализации потребуется массив для хранения элементов и два индекса указывающих на начало и конец очереди, head и tail соответственно.


Изображение иллюстрирует структуру очереди на основе массива

Код ниже демонстрирует объявление очереди:

123456789

// Очередь на основе массива.
// head     - индекс указывающий на первый элемент в очереди
// tail     - индекс указывающий на последний элемент очереди
// elements - массив элементов очереди
type Queue[T any] struct {
  head     int
  tail     int
  elements []T
}

Добавление нового элемента осуществляется в следующую свободную ячейку после tail:

1. Сдвинуть tail на следующую доступную позицию.

2. Добавить новый элемент в ячейку с индексом tail.


Изображение иллюстрирует добавление нового элемента в очередь

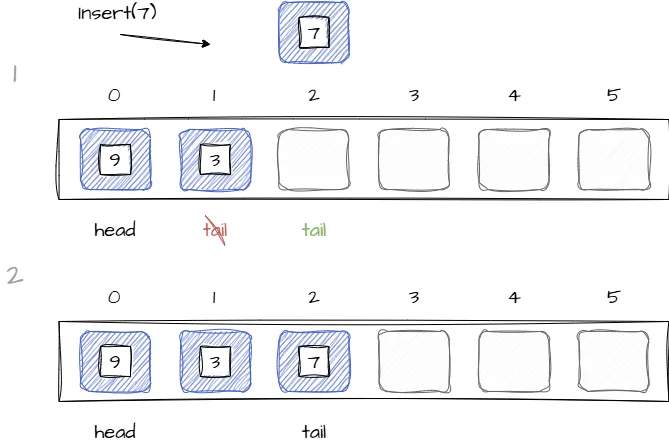
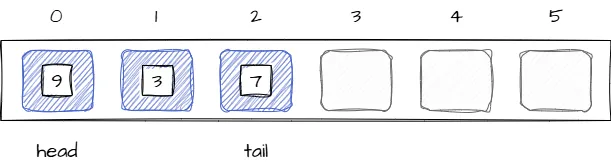
В случае когда индекс tail достиг границы массива и в самом начале очереди есть свободные ячейки после удаления элементов, тогда новый элемент может занять одну из свободных ячеек, индекс tail будет указывать на добавленный элемент. Изображение ниже иллюстрирует описанный сценарий:


Изображение иллюстрирует перенос элемента в начало массива при достижении его границ

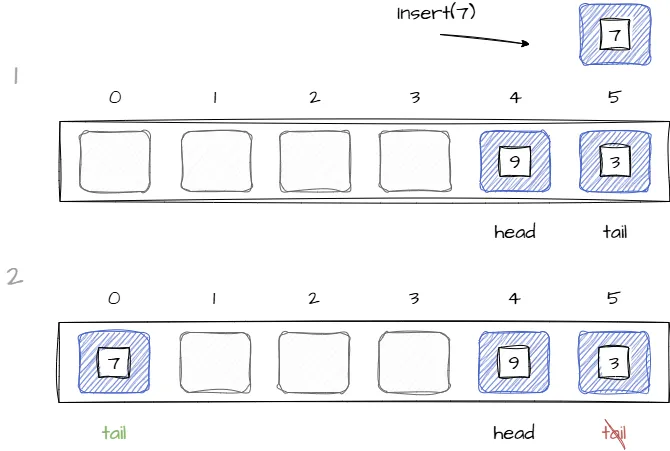
Если индекс tail достиг границы массива и в самом начале нет свободных ячеек, тогда необходимо создать новый массив большего размера, а все элементы старого скопировать в него. Код ниже реализует добавление нового элемента в конец очереди:

12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152

// Кол-во элементов, которое будет выделено при достижении границы массива.
const ALLOCATE_SIZE = 10

// Добавление нового элемента в конец очереди.
// element - добавляемый элемент
func (queue *Queue[T]) Insert(element T) {
  // При первом добавлении элемента необходимо инициализировать
  // индексы начальными значениями
  size := len(queue.elements)
  if size == 0 {
    queue.head = 0
    queue.tail = -1
  }

  // Если исчерпали свободные ячейки для добавления, то необходимо расширить
  // массив на ALLOCATE_SIZE, значения при этом должны быть скопированны
  // в новый массив
  index := queue.tail + 1
  if (index >= size && queue.head == 0) || index == queue.head {
    allocated := make([]T, size+ALLOCATE_SIZE)

    headIndex := 0
    if size > 0 {
      // Копирование элементов от head и до конца массива
      for headIndex+queue.head < size {
        allocated[headIndex] = queue.elements[headIndex+queue.head]
        headIndex++
      }

      // Копирование элементов от начала массива и до tail, только в
      // том случае, если начало очереди не совпадает с началом массива
      if queue.tail < queue.head {
        tailIndex := 0
        for tailIndex <= queue.tail {
          allocated[headIndex] = queue.elements[tailIndex]
          headIndex++
          tailIndex++
        }
      }
    }
    queue.head = 0
    index = headIndex
    queue.elements = allocated
    // Если достигли конца массива, но в самом начале есть пустые ячейки
    // для добавления элементов, тогда необходимо перейти в начало массива
  } else if index >= size && queue.head > 0 {
    index = 0
  }

  queue.tail = index
  queue.elements[index] = element
}

В строках 10-13 индексы head и tail инициализируются начальными значениями, в том случае если очередь была пуста. В строках 19-46 массив расширяется путем создания нового с копированием всех значений в него. Для удаления элемента из очереди индекс head необходимо сдвинуть на одну ячейку вперед, при этом значение в ячейке остается до тех пор, пока не будет перезаписано новым значением.


Изображение иллюстрирует удаление элемента из очереди

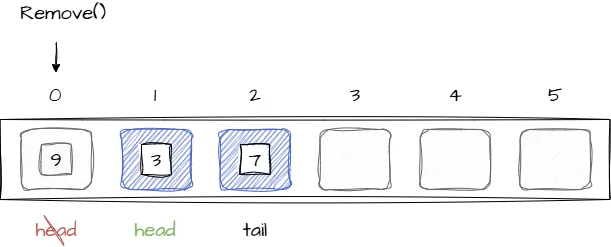
В случае, когда индекс head достиг границы массива, происходит перенос в начало аналогично операции добавления, следующий код реализует удаление элемента из очереди:

1234567891011121314151617181920212223242526

// Удаление элемента из очереди, возвращает значение первого элемента или
// выбрасывает ошибку, если очередь пуста.
func (queue *Queue[T]) Remove() T {
  // Если очередь содержит элементы, то обработка продолжается,
  // иначе выбрасываем ошибку
  size := len(queue.elements)
  if size > 0 && queue.tail >= 0 {
    value := queue.elements[queue.head]

    // Если достигли конца массива, но в самом начале есть элементы,
    // тогда необходимо перейти в начало массива
    index := queue.head + 1
    if index >= size && queue.head > queue.tail {
      index = 0
      // Если извлекли последний элемент, то возвращаем индексы
      // к начальным значениям
    } else if queue.head == queue.tail {
      index = 0
      queue.tail = -1
    }
    queue.head = index

    return value
  }
  panic("queue is empty")
}

Сравнение реализаций

В реализации на основе массива добавление и удаление выполняется за константное время O(1), исключая редкий сценарий полного заполнения массива при котором необходимо копирование всех элементов за O(n), где n количество элементов в массиве. Массив требует значительно меньше памяти для хранения элементов и благодаря своей структуре позволяет реализовать больше полезных сценариев, например обращение к n-ому элементу очереди, что не получится сделать в связном списке без перебора элементов. Описанные операции в очереди на основе связного списка выполняются за O(1). Главное преимущество данной реализации заключается в простоте, тем не менее, ей требуется больше памяти и обращение к n-ому элементу очереди не получится сделать без перебора элементов, которое будет выполнено за O(n).

Весь исходный код примеров к данной статье вы можете найти на GitHub.